- La función definida por
 , tiene como dominio, codominio e imagen a todos los números reales
, tiene como dominio, codominio e imagen a todos los números reales 
- Para la función
 tal que
tal que  , en cambio, si bien su dominio y codominio son iguales a
, en cambio, si bien su dominio y codominio son iguales a  , sólo tendrá como imagen los valores comprendidos entre 0 y +∞.
, sólo tendrá como imagen los valores comprendidos entre 0 y +∞.
- En la figura se puede apreciar una función
 , con
, con
- Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el 1 y el 4). Finalmente,
- Esta función representada como relación, queda:

- Yo entendi que las funciones reales en muchos casos puede darse de dos condiciones, como podemos observar en el ejemplo anterior todos los elementos de x estan relacionados con los elementos de y, ademas el conjunto de x y y se forman entre si para formar o componer un solo conjunto. La grafica de una funcion esta formada por todos los puntos x y y donde y pertenece al dominio de f y x= a la distancia dirijida desde el eje y, f(x)= distancia dirijida desde el eje x.


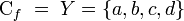

No hay comentarios:
Publicar un comentario